Χάος
- «Μεταδίδει στον αναγνώστη την πνευματική απόλαυση που συνοδεύει τις νέες ιδέες για τη σχέση ανάμεσα στην απλότητα των φυσικών νόμων και την πολυπλοκότητα του κόσμου μας.» -- Nature
- «Γοητευτικές ιστορίες ενοράσεως και ανακαλύψεων, γραμμένες με δραματική διάθεση και ερεθιστικό τρόπο. Σχεδόν κάθε παράγραφός του περιλαμβάνει και ένα ξάφνιασμα.» -- The New York Times
- «Ένα θαυμάσιο εισαγωγικό βιβλίο για μια καυτή περιοχή έρευνας. Δεν εξηγεί μόνο με ακρίβεια και επιδεξιότητα τις θεμελιώδεις έννοιες της θεωρίας του χάους, αλλά και περιγράφει γλαφυρά την ιστορία της πρωτοποριακής έρευνας και το παρασκήνιό της.» -- Martin Gardner
Ένα βιβλίο που καλύπτει ολόκληρη την ιστορία της ανάπτυξης της θεωρίας του χάους και πολλές πλευρές της με τον συγγραφέα να έχει κάνει εκτενή έρευνα αλλά που σίγουρα απευθύνεται σε ανθρώπους με υπόβαθρο μαθηματικών ή φυσικής και δε θα το συνιστούσα στο μέσο αναγνώστη και σίγουρα όχι σε αναγνώστες κάτω των 16 ετών. Το βιβλίο είναι μια πολύ καλή δουλειά μεγάλης αξίας για τον ενδιαφερόμενο αλλά αρκετά τεχνικό για κάποιον χωρίς κάποιες ακαδημαϊκές γνώσεις που να σχετίζονται με το θέμα. Ένα χρήσιμο βιβλίο αλλά όχι ευχάριστο για την αναγνωστική πλειοψηφία.
Κάντο όπως ο Beckham! (ή, τουλάχιστον, δες πώς το καταφέρνει!)
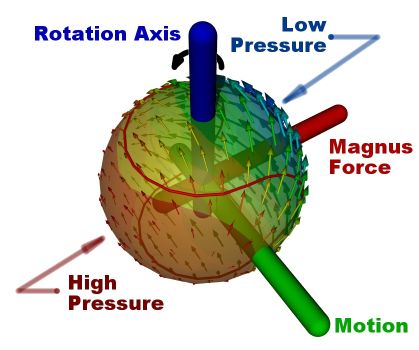Ο Bill Shankly, ένας από τους πιο επιτυχημένους, αλλά και αγαπημένους προπονητές της ποδοσφαιρικής ομάδας του Liverpool, έλεγε κάποτε ότι "αν ένας παίκτης δεν παρεμβάλλεται στο παιχνίδι ή δεν προσπαθεί να αποκομίσει κάποιο πλεονέκτημα, τότε θα έπρεπε να το κάνει!". Η αλήθεια είναι ότι στο σύγχρονο ποδόσφαιρό, αλλά γενικά στον αθλητισμό, είναι σχεδόν αδύνατο να αποκομίσει κανείς κάποιο πλεονέκτημα χωρίς να παραβεί τους κανόνες. Ο Beckham, ο Woods, ο Federer, αλλά και ο Παναγιώτης Γιαννάκης κατάφεραν να βρίσκονται για χρόνια στην κορυφή του αθλήματός τους κυρίως χάρη στην ικανότητά τους να μεταβάλλουν την πορεία της μπάλας, βάζοντάς της φάλτσο. Δείτε πώς αυτό που στη φυσική ονομάζεται "φαινόμενο Magnus", γίνεται ο μεγαλύτερος φόβος ενός τερματοφύλακα!
Το παράδοξο των γενεθλίων
Σκεφτείτε πως έχετε σε ένα δωμάτιο μια ομάδα ατόμων και κάνετε μια δημοσκόπηση για την ημερομηνία των γενεθλίων τους. Όπως περιμένει κανείς, όσο περισσότερα είναι τα άτομα αυτά, τόσο μεγαλύτερη είναι η πιθανότητα να συμπίπτουν οι ημερομηνίες γενεθλίων για δύο από αυτά. Θα περίμενε όμως κανείς ότι η πιθανότητα αυτή ξεπερνάει το 50% για 23 άτομα, ενώ για 57 γίνεται πάνω από 99%;
RSS Feeds/Ροές δεδομένων: 
